Abstract
Optimal sanitary policies based on a simulated SIRD model depends extensively on the value of R0. So a statistical analysis is made necessary to take into account the diversity of situations. And similar policies led in different countries do not lead to the same result. In Gallic et al. (2021), we model the dynamics of mortality due to Covid with a double sigmoid model. Coupled with an adjusted SIRD model and policy data from the Oxford Blavatnik School of Government, we can measure the economic cost of lock-down in ten European countries over the first two waves of the pandemic, together with the cost in term of deaths and the psychological cost. There does not seem to exist a trade-off between the economic cost of a lock-down and the number of deaths.
The results
If we leave aside the case of Iceland, anti-Covid policies in Europe during the first two waves were relying either on herd-immunity (for Sweden and the Netherlands) or on crushing the curve to avoid ICU saturation (for the other European countries). The available tools at that time relied on social distancing, confinement, information of the public as no vaccine was yet available. The implemented lock-downs were more or less stringent, depending on the objective (ICU or herd immunity) and of course on the strength of the waves. The diversity of situations and policy reaction is well illustrated in Figure 1.
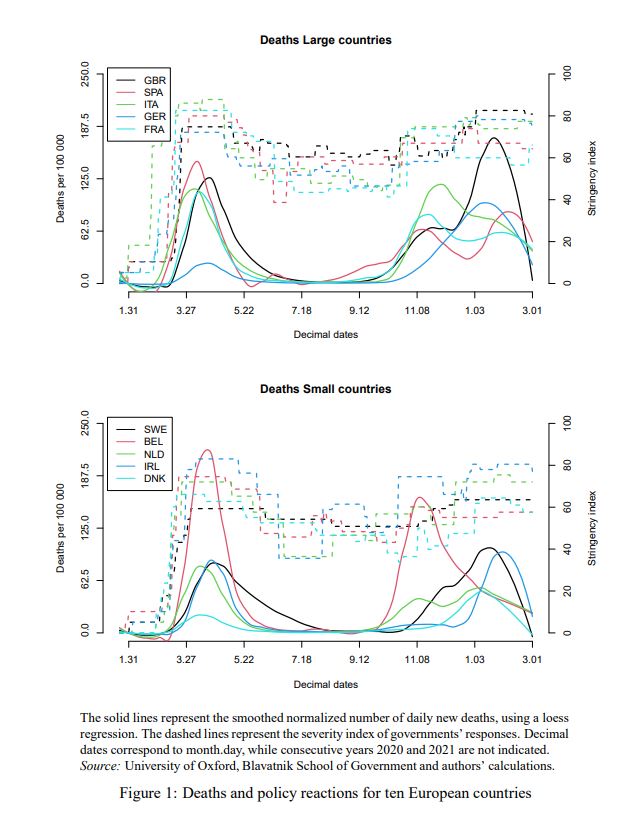
Although effective in containing the epidemic, a lock-down has some unwanted consequences. From an epidemiologic point of view (Ferguson et al. 2020, Salje et al. 2020), a sub-optimal confinement can lead to a rebound and a second wave. On the other side, economists prefer to insist on the economic cost of a lock-down that has to be put in balance to the number of deaths leading to some kind of trade-off (Gollier (2020), Acemoglu et al. 2020). A third type of adverse consequences is psychological cost as main sanitary measures are based on social distancing. This cost is not often measured.
In Gallic et al. (2021), we calibrate the SIRD model of Kermack and McKendrick (1927) and define two loss functions in order to design an optimal lock-down depending on the objective, the value of R0 and the starting date measured as a distance to the peak of the wave. We report the implied number of deaths and the economic loss, following both the epidemiologic tradition and the economic point of view. An efficient lock-down has first to avoid a possible rebound (overshooting) and second to reduce the value of the effective reproduction number and consequently the number of deaths. However the optimal triplet starting date, severity and length depends very much on local conditions. The availability of a vaccine of course changes very much the problem. So we limit our attention to examining ten European countries between January 2020 and March 2021. The Oxford Blavatnik School of Government collected data both on the number of deaths and at the same time on the severity of lock-down policies. Taking advantage on the close relation between SIR models and phenomenological models coming from the biological literature on the growth of species (Wang et al. 2012), we used a double sigmoid model to model the dynamics of the epidemics in the presence of lock-downs over two waves. We provide for each country an estimation for the effective reproduction number which serves to calibrate a SIRD model in order to measure the production loss during the period of confinements. As a result, we obtain Table 1, from which we can compare the efficiency of confinement policies in 10 European countries. The psychological cost corresponds to the product between lock-down length and intensity.
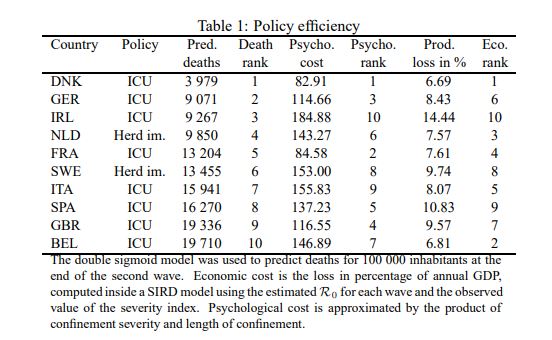
Denmark, applying an ICU policy, obtained the best results according to all criteria, probably thanks to an initial small R0 and an early reaction. Germany also managed to limit the number of deaths thanks to an initial moderate R0 and an early reaction. When comparing the UK and Germany, Pesaran and Yang (2020) insisted a lot on an early start. Germany managed to limit the psychological cost, but not the economic cost, compared to other countries (Denmark, the Netherlands, France, Belgium). Ireland managed to minimize the number of deaths, but at a huge economic cost, the largest of the list. France privileged the psychological cost, but is roughly equally ranked for deaths and economic cost. When comparing sanitary efficiency within this group of countries that have applied similar policies, there does not seem to exist a trade-off between lives and economic cost, as emphasized in the recent economic literature (Acemoglu et al. 2020, Alvarez et al. 2020, Gollier 2020, Gori et al. 2021). For instance, Great Britain had a very high death rate together with a high economic cost as well as Spain. The case of Belgium is difficult to interpret as this country had an extensive counting method for the origin of deaths.
The question of the efficiency of policies based on herd immunity is easy to clear out in Table 1. Sweden has maintained its herd immunity policy over the two waves. It does not seem to have been particularly efficient as it cumulates high death rates, high economic and psychological costs. The Netherlands apparently decided to change their policy between the two waves with more severe measures despite a lower R0. Moreover, they had a quicker reaction at the beginning of the first wave, contrary to Sweden which was late. They were apparently right because at the end they were better than Sweden for deaths despite a higher R0 and they also manage to minimize the economic and psychological costs.
SIRD models are difficult to use for designing an optimal sanitary policy as their calibration is most of time based on average values and thus does not reflect the diversity of local situations. However, they can be used in conjunction with statistical models as we do in Gallic et al. (2021). From our experience, it is dangerous to justify a natural herd immunity policy on the basis of a SIRD model. These policies mean that a confinement has to start as close to the peak as possible when we have seen that countries with a quick sanitary policy were much more successful. Finally, all those models do not take into account geography to model the transmission of the disease when germs totally ignore frontiers. In this domain, Hafner (2020) is a first step toward taking into account spatial analysis for modelling the propagation of epidemics.
References
Acemoglu, D., Chernozhukov, V., Werning, I., and Whinston, M. D. , 2020, "Optimal targeted lockdowns in a multi-group SIR model". Discussion paper, MIT Economic Department.
Alvarez, F. E., Argente, D., and Lippi, F. ,2020, "A simple planning problem for COVID-19 lockdown". Working Paper 26981, NBER.
Ferguson, N. M., Laydon, D., Nedjati-Gilani, G., Imai, N., Ainslie, K., Baguelin, M., Bhatia, S., Boonyasiri, A., Cucunuba, Z., Cuomo-Dannenburg, G., Dighe, A., Dorigatti, I., Fu, H., Gaythorpe, K., Green, W., Hamlet, A., Hinsley, W., Okell, L. C., van Elsland, S., Thompson, H., Verity, R., Volz, E., Wang, H., Wang, Y., Walker, P. G., Walters, C., Winskill, P., Whittaker, C., Donnelly, C. A., Riley, S., and Ghani, A. C., 2020, "Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand." Report 9, Imperial College.
Gallic, E., Lubrano, M., and Michel, P., 2021, "Optimal lockdowns for Covid-19 pandemics: Analyzing the efficiency of sanitary policies in Europe". Journal of Public Economic Theory, 1–24.
Gollier C., 2020, "Cost–benefit analysis of age-specific deconfinement strategies." Journal of Public Economic Theory, 22(6):1746–1771.
Gori, L., Manfredi, P., Marsiglio, S., and Sodini, M. , 2021, "Covid-19 epidemic and mitigation policies: Positive and normative analyses in a neoclassical growth model". Journal of Public Economic Theory
Hafner C., 2020, "The spread of the Covid-19 pandemic in time and space". International Journal of Environmental Research and Public Health, 17(11):3827.
Kermack, W. O. and McKendrick, A. G., 1927, "A contribution to the mathematical theory of epidemics." Proceedings of the Royal Society A, 115(772):700–721.
Pesaran, H. and Yang, C., 2020, "Matching theory and evidence on Covid-19 using a stochastic model of epidemics on networks." Technical report, University of Southern California.
Salje, H., Tran Kiem, C., Lefrancq, N., Courtejoie, N., Bosetti, P., Paireau, J., Andronico, A., Hoz´e, N., Richet, J., Dubost, C.-L., Le Strat, Y., Lessler, J., Levy-Bruhl, D., Fontanet, A., Opatowski, L., Boelle, P.-Y., and Cauchemez, S., 2020, "Estimating the burden of SARSCoV-2 in France." Science, 369:208–211.
Wang, X.-S., Wu, J., and Yang, Y., 2012, "Richards model revisited: Validation by and application to infection dynamics." Journal of Theoretical Biology, 313:12–19.